MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [742]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

Em uma teoria relativística da física, um escalar de Lorentz é uma expressão, formada a partir de itens da teoria, que resulta em um escalar, invariante sob qualquer transformação de Lorentz. Um escalar de Lorentz pode ser gerado a partir, por exemplo, do produto escalar de vetores ou da contração de tensores da teoria. Enquanto os componentes de vetores e tensores são, em geral, alterados sob transformações de Lorentz, os escalares de Lorentz permanecem inalterados.

Um escalar de Lorentz nem sempre é imediatamente visto como um escalar invariante no sentido matemático, mas o valor escalar resultante é invariante sob qualquer transformação de base aplicada ao espaço vetorial, no qual se baseia a teoria considerada. Um escalar de Lorentz simples no espaço-tempo de Minkowski é a distância no espaço-tempo ("comprimento" de sua diferença) de dois eventos fixos no espaço-tempo. Enquanto os quadrivetores de "posição" dos eventos mudam entre diferentes referenciais inerciais, sua distância no espaço-tempo permanece invariante sob a transformação de Lorentz correspondente. Outros exemplos de escalares de Lorentz são o "comprimento" de quadrivelocidades (veja abaixo), ou a curvatura de Ricci em um ponto no espaço-tempo da relatividade geral, que é uma contração do tensor de curvatura de Riemann ali.

Escalares simples na relatividade especial

O comprimento de um vetor de posição

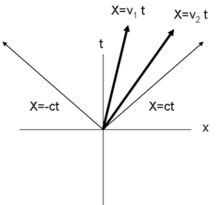
Na relatividade especial, a localização de uma partícula no espaço-tempo quadridimensional é dada por

x^{\mu }=(ct,\mathbf {x} )

onde $\mathbf {x} =\mathbf {v} t$ é a posição no espaço tridimensional da partícula, $\mathbf {v}$ é a velocidade no espaço tridimensional e $�$ é a velocidade da luz.

O "comprimento" do vetor é um escalar de Lorentz e é dado por

x_{\mu }x^{\mu }=\eta _{\mu \nu }x^{\mu }x^{\nu }=(ct)^{2}-\mathbf {x} \cdot \mathbf {x} \ {\stackrel {\mathrm {def} }{=}}\ (c\tau )^{2}

onde $\tau$ é o tempo adequado medido por um relógio no referencial de repouso da partícula e a métrica de Minkowski é dada por

\eta ^{\mu \nu }=\eta _{\mu \nu }={\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}.

Esta é uma métrica semelhante ao tempo.

Frequentemente, a assinatura alternativa da métrica de Minkowski, na qual os sinais dos uns são invertidos, é usada.

\eta ^{\mu \nu }=\eta _{\mu \nu }={\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}.

Esta é uma métrica semelhante ao espaço.

Na métrica de Minkowski, o intervalo espacial $�$ é definido como

x_{\mu }x^{\mu }=\eta _{\mu \nu }x^{\mu }x^{\nu }=\mathbf {x} \cdot \mathbf {x} -(ct)^{2}\ {\stackrel {\mathrm {def} }{=}}\ s^{2}.

Usamos a métrica de Minkowski semelhante ao espaço no restante deste artigo.

O comprimento de um vetor de velocidade

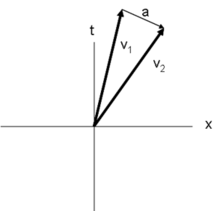
A velocidade no espaço-tempo é definida como

v^{\mu }\ {\stackrel {\mathrm {def} }{=}}\ {dx^{\mu } \over d\tau }=\left(c{dt \over d\tau },{dt \over d\tau }{d\mathbf {x}  \over dt}\right)=\left(\gamma c,\gamma {\mathbf {v} }\right)=\gamma \left(c,{\mathbf {v} }\right)

onde

\gamma \ {\stackrel {\mathrm {def} }{=}}\ {1 \over {\sqrt {1-{{\mathbf {v} \cdot \mathbf {v} } \over c^{2}}}}}.

A magnitude da quadrivelocidade é um escalar de Lorentz,

v_{\mu }v^{\mu }=-c^{2}\,.

Portanto, c é um escalar de Lorentz.

O produto interno da aceleração e da velocidade

A quadriaceleração é dada por

a^{\mu }\ {\stackrel {\mathrm {def} }{=}}\ {dv^{\mu } \over d\tau }.

A quadriaceleração é sempre perpendicular à quadrivelocidade

0={1 \over 2}{d \over d\tau }\left(v_{\mu }v^{\mu }\right)={dv_{\mu } \over d\tau }v^{\mu }=a_{\mu }v^{\mu }.

Portanto, podemos considerar a aceleração no espaço-tempo simplesmente como uma rotação da quadrivelocidade. O produto interno da aceleração e da velocidade é um escalar de Lorentz e é zero. Esta rotação é simplesmente uma expressão de conservação de energia:

{dE \over d\tau }=\mathbf {F} \cdot \mathbf {v}

onde $�$ é a energia de uma partícula e $\mathbf {F}$ é a triforça na partícula.

Energia, massa em repouso, trimomento e trivelocidade a partir do quadrimomento

O quadrimomento de uma partícula é

p^{\mu }=mv^{\mu }=\left(\gamma mc,\gamma m\mathbf {v} \right)=\left(\gamma mc,\mathbf {p} \right)=\left({\frac {E}{c}},\mathbf {p} \right)

onde $�$ é a massa de repouso da partícula, $\mathbf {p}$ é o momento no espaço tridimensional e

E=\gamma mc^{2}

é a energia da partícula.

Medição da energia de uma partícula

p_{\mu }u^{\mu }=-E_{1}

onde o subscrito 1 indica a primeira partícula.

Como a relação é verdadeira no referencial de repouso da segunda partícula, ela é verdadeira em qualquer referencial. $E_{1}$ , a energia da primeira partícula no referencial da segunda partícula, é um escalar de Lorentz. Portanto,

E_{1}=\gamma _{1}\gamma _{2}m_{1}c^{2}-\gamma _{2}\mathbf {p} _{1}\cdot \mathbf {u} _{2}

em qualquer referencial inercial, onde $E_{1}$ ainda é a energia da primeira partícula no referencial da segunda partícula.

Medição da massa de repouso da partícula

No referencial de repouso da partícula, o produto interno do momento é

p_{\mu }p^{\mu }=-(mc)^{2}\,.

Portanto, a massa de repouso ( $m$ ) é um escalar de Lorentz. A relação permanece verdadeira independentemente do referencial no qual o produto interno é calculado. Em muitos casos, a massa de repouso é escrita como $m_{0}$ para evitar confusão com a massa relativística, que é $\gamma m_{0}$ .

Medição do trimomento da partícula

Observe que

\left({\frac {p_{\mu }u^{\mu }}{c}}\right)^{2}+p_{\mu }p^{\mu }={E_{1}^{2} \over c^{2}}-(mc)^{2}=\left(\gamma _{1}^{2}-1\right)(mc)^{2}=\gamma _{1}^{2}{\mathbf {v} _{1}\cdot \mathbf {v} _{1}}m^{2}=\mathbf {p} _{1}\cdot \mathbf {p} _{1}.

O quadrado da magnitude do trimomento da partícula medido no referencial da segunda partícula é um escalar de Lorentz.

Medição da trivelocidade da partícula

A trivelocidade, no referencial da segunda partícula, pode ser construída a partir de dois escalares de Lorentz

v_{1}^{2}=\mathbf {v} _{1}\cdot \mathbf {v} _{1}={\frac {\mathbf {p} _{1}\cdot \mathbf {p} _{1}}{E_{1}^{2}}}c^{4}.

Escalares mais complicados

Os escalares também podem ser construídos a partir dos tensores e vetores, da contração de tensores (como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

////// $F_{\mu \nu }F^{\mu \nu }$ ) ou combinações de contrações de tensores e vetores (como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

////// $g_{\mu \nu }x^{\mu }x^{\nu }$ ).

Em física, a ação de Polyakov é a ação bidimensional de uma teoria conforme de campos (CFT en inglés)^[1] descrevendo a variedade^{[nota 1]} bidimensional^[2] que descreve a incorporação de uma corda no espaço-tempo na teoria das cordas. ^[3] ^[4] ^[5]

Esta ação foi introduzida por Stanley Deser e Bruno Zumino ^[6] e, independentemente, por L.Brink, Vecchia P.Di e PSHowe, ^[7] e passou a ser associada com Alexander Polyakov depois que ele fez uso dela na quantificação da corda.^[8]

A ação lê

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {S}}={T \over 2}\int \mathrm {d} ^{2}\sigma {\sqrt {-h}}h^{ab}g_{\mu \nu }(X)\partial _{a}X^{\mu }(\sigma )\partial _{b}X^{\nu }(\sigma )

onde $�$ é a tensão da corda, $g_{\mu \nu }$ é a métrica da variedade alvo^{[nota 2]}, $h_{ab}$ é a folha de universo métrica e $ℎ$ é o determinante de ${ab}$ . A assinatura métrica é escolhido de tal modo que direções similares ao tempo são + e direções como espaço são -. A coordenada de folha de universo tipo espacial é chamada $\sigma$ ao passo que a coordenada de folha de universo tipo tempo é chamada $\tau$ . Esta variedade é também conhecida como modelo σ não-linear.^[9]

A ação de Polyakov deve ser completada pela ação de Liouville na teoria de campo de Liouville para descrever adequadamente as flutuações de cordas.

Relação com a ação Nambu-Goto

Escrevendo a equação de Euler-Lagrange para o tensor métrico $h^{ab}$ se obtém que:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\frac {\delta S}{\delta h^{ab}}}=T_{ab}=0

Sabendo também que:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\delta {\sqrt {-h}}=-{\frac {1}{2}}{\sqrt {-h}}h_{ab}\delta h^{ab}

Pode-se escrever o derivativo variacional da ação:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\frac {\delta S}{\delta h^{ab}}}={\frac {T}{2}}{\sqrt {-h}}\left(G_{ab}-{\frac {1}{2}}h_{ab}h^{cd}G_{cd}\right)

onde $G_{ab}=g_{\mu \nu }\partial _{a}X^{\mu }\partial _{b}X^{\nu }$ o que leva a:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

T_{ab}=T\left(G_{ab}-{\frac {1}{2}}h_{ab}h^{cd}G_{cd}\right)=0

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

G_{ab}={\frac {1}{2}}h_{ab}h^{cd}G_{cd}

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

G=\mathrm {det} \left(G_{ab}\right)={\frac {1}{4}}h\left(h^{cd}G_{cd}\right)^{2}

Se o tensor métrico auxiliar da folha de universo ${\sqrt {-h}}$ é calculado a partir das equações de movimento:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\sqrt {-h}}={\frac {2{\sqrt {-G}}}{h^{cd}G_{cd}}}

e substituído de volta à ação, ele se torna a ação Nambu-Goto:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

S={T \over 2}\int \mathrm {d} ^{2}\sigma {\sqrt {-h}}h^{ab}G_{ab}={T \over 2}\int \mathrm {d} ^{2}\sigma {\frac {2{\sqrt {-G}}}{h^{cd}G_{cd}}}h^{ab}G_{ab}=T\int \mathrm {d} ^{2}\sigma {\sqrt {-G}}

No entanto, a ação de Polyakov é mais facilmente quantificada porque é linear.

A ação Nambu-Goto é uma quantidade matemática que pode ser usada para predizer como as cordas se movem através do espaço e do tempo.

Ela é a ação mais simples que descreve uma corda relativistica^[1] Pela aplicação das ideias da mecânica quântica às ações Nambu-Goto (um procedimento conhecido como quantização) pode-se deduzir que cada corda pode vibrar em muitos diferentes modos, e que cada estado vibracional representa uma partícula diferente.^[2] Esta ação é a mais simples invariante ação na teoria das cordas bosônica.^[3] Ela, para uma corda clássica, a qual possui claramente uma interpretação geométrica, a partir desta ação, que se deduz uma ação mais geral, a ação de Polyakov, e pode ser demonstrado que estas duas são classicamente equivalentes. A ação Nambu-Goto também é usada em outras teorias que investigam objetos-cordas (por exemplo, cordas cósmicas)^{[nota 1]}. É o ponto de partida da análise de comportamento zero-espessura (infinitamente fina) das cordas, usando os princípios da mecânica de Lagrange.^[4] Assim como a ação para uma partícula de ponto livre é proporcional ao seu tempo apropriado, ou seja, o "tamanho" de seu mundo-linha, uma relativista ação da corda é proporcional à área da folha que a corda traça, enquanto que viaja através do espaço-tempo.^[5] A ação deve o seu nome aos físicos japoneses Yoichiro Nambu e Goto Tetsuo.^[6]

Definição

A ação Nambu-Goto é uma ação funcional para modelos sigma^[7] com o espaço alvo uma pseudo variedade de Riemann^[8]^[9] $(X,g)(X,g)$ : Isto é o volume induzido funcional

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$S_{NG}:(\Sigma {\stackrel {\gamma }{\to }}X)\mapsto \int _{\Sigma }dvol(\gamma ^{*}g)\,,$

onde $dvol(\gamma ^{*}g)$ é a forma de volume^[10]^[11] da retração $(\gamma ^{*}g)$ do tensor métrico a partir de $�$ para $\Sigma$ .^[12]

Folha de universo

Assim como um zero-dimensional traça um mundo-linha em um diagrama espaço-tempo, uma corda unidimensional é representada por uma folha de universo.^[13]

Yoichiro Nambu (2008)

Todas as folha de universo são superfícies bidimensionais, e requerem dois parâmetros para especificar um ponto na folha. Os teóricos das cordas usam os símbolos τ e σ para estes parâmetros. Como se vê, as teorias de cordas envolvem superiores espaços dimensionais que o do mundo 3D com o qual estamos familiarizados; teoria das cordas bosônicas requer 25 dimensões espaciais e um eixo de tempo. Se d é o número de dimensões espaciais, podemos representar um ponto pela vector

x=(x^{0},x^{1},x^{2},\ldots ,x^{d}).

Descrevemos uma corda usando funções que mapeiam uma posição no espaço paramétrico (τ, σ) para um ponto no espaço-tempo. Para cada valor de τ e σ, estas funções especificam um único vetor espaço-tempo:

X(\tau ,\sigma )=(X^{0}(\tau ,\sigma ),X^{1}(\tau ,\sigma ),X^{2}(\tau ,\sigma ),\ldots ,X^{d}(\tau ,\sigma )).

As funções $X^{\mu }(\tau ,\sigma )$ determinam a forma que a folha de universo toma. Diferentes Lorentz observadores vão discordar sobre as coordenadas que atribuem a pontos particulares n a folha de universo, mas todos eles devem concordar com a área total que a folha de universo possui. A ação Nambu-Goto é escolhida para ser proporcional a esta área total.

Deixe $g_{\ mu\ nu}$ ser a métrica (d +1)-espaço-tempo dimensional. Então,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

g_{ab}=g_{\mu \nu }{\frac {\partial X^{\mu }}{\partial \sigma ^{a}}}{\frac {\partial X^{\nu }}{\partial \sigma ^{b}}}\

é a métrica induzida ^{[nota 2]} na a folha de universo da corda.

A área ${\mathcal {A}}$ d a folha de universo é dada por:

\mathrm {d} {\mathcal {A}}=\mathrm {d} ^{2}\Sigma {\sqrt {-g}}

onde $\mathrm {d} ^{2}\Sigma =\mathrm {d} \sigma \,\mathrm {d} \tau$ e $g=\mathrm {det} \left(g_{ab}\right)\$

Usando a notação que:

{\dot {X}}={\frac {\partial X}{\partial \tau }}

X'={\frac {\partial X}{\partial \sigma }},

pode-se reescrever a métrica $g_{ab}$ :

g_{ab}=\left({\begin{array}{cc}{\dot {X}}^{2}&{\dot {X}}\cdot X'\\X'\cdot {\dot {X}}&X'^{2}\end{array}}\right)\

g={\dot {X}}^{2}X'^{2}-({\dot {X}}\cdot X')^{2}

a ação Nambu-Goto é definida como,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {S}}\

=-{\frac {T_{0}}{c}}\int d{\mathcal {A}}

=-{\frac {T_{0}}{c}}\int \mathrm {d} ^{2}\Sigma {\sqrt {-g}}

=-{\frac {T_{0}}{c}}\int \mathrm {d} ^{2}\Sigma {\sqrt {({\dot {X}}\cdot X')^{2}-({\dot {X}})^{2}(X')^{2}}}.\

Os fatores antes da integral dá a ação as unidades corretas, energia multiplicada pelo tempo. T₀ é a tensão na corda, e c é a velocidade da luz. Normalmente, os teóricos das cordas trabalho em "unidades naturais", onde c é definida como 1 (juntamente com $\hbar$ constante de Planck e constante G de Newton). Também, em parte por razões históricas, eles usam o "parâmetro de declive" $\alpha '$ em vez de T₀. Com estas mudanças, a ação Nambu-Goto torna-se

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {S}}=-{\frac {1}{2\pi \alpha '}}\int \mathrm {d} ^{2}\Sigma {\sqrt {({\dot {X}}\cdot X')^{2}-({\dot {X}})^{2}(X')^{2}}}.

Estas duas formas são, naturalmente, inteiramente equivalentes: escolher uma sobre a outra é uma questão de convenção e conveniência.

Duas outras formas equivalentes são

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {S}}=-{\frac {1}{2\pi \alpha '}}\int \mathrm {d} ^{2}\Sigma {\sqrt {{\dot {X}}^{2}-{X'}^{2}}},

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {S}}=-{\frac {1}{4\pi \alpha '}}\int \mathrm {d} ^{2}\Sigma ({\dot {X}}^{2}-{X'}^{2}).

Normalmente, a ação Nambu-Goto não descreve a correta física quântica da corda. Para isso, deve ser modificada de uma forma semelhante como a ação de uma partícula ponto. Ela é classicamente igual a menos massa vezes o comprimento invariante no espaço-tempo, mas deve ser substituído por uma expressão quadrática com o mesmo valor clássica. Só então que a física quântica correta é obtida.^[14] Para cordas, a correção analógico é fornecida pela ação Polyakov, que é classicamente equivalente à ação Nambu-Goto, mas dá a teoria quântica correta. É, no entanto, possível desenvolver uma teoria quântica da ação Nambu-Goto no Medidor de cone-de-luz.

Em geometria diferencial, tensor de curvatura é uma das noções métricas mais importantes. Um tensor de curvatura é uma generalização da curvatura de Gauss em dimensões mais altas (dois exemplos disto são o tensor de Riemann que se desenvolve neste artigo e o tensor de Ricci).

A geometria infinitesimal das variedades de Riemann com dimensão ≥ 3 é demasiado complicada para ser descrita totalmente por um número em um ponto dado (tal como sucede quando a dimensão é menor ou igual a 2). Assim em 2 dimensões a curvatura pode ser representada por um número escalar (ou tensor de ordem zero), em 3 dimensões a curvatura pode ser representada por um tensor de segunda ordem (como por exemplo o tensor de Ricci). Entretanto para dimensões totalmente gerais se necessita ao menos um tensor de quarta ordem (como o tensor de Riemann). Foi Riemann quem introduziu uma maneira de descrever completamente a curvatura em qualquer número de dimensões mediante um "pequeno monstro" de tensor, chamado tensor de Riemann.

Descrição

Definição geral

Seja $�$ uma variedade diferenciável dotada de uma conexão $\nabla$ , definida em um ponto $�$ da variedade. O tensor de Riemann é o campo tensorial $�$ de tipo (1,3) que satisfaz a igualdade

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z$ ,

em que $�, �, �$ são campos vetoriais em $M_{p}$ , sendo $[X,Y]$ o colchete de Lie dos campos vetoriais. $R(X,Y)Z$ é linear em $�, �, �$ , de modo que o valor de $R(X,Y)Z$ em $�$ só depende dos valores de $�, �$ e $�$ em $�$ .^[1] É importante destacar que o tensor de Riemann é algumas vezes representado pelo sinal oposto.

O teorema de Schwarz afirma que no espaço euclidiano as derivadas parciais comutam: este fato não é verdade em uma variedade com conexão arbitrária, e o tensor de Riemann leva isso em consideração. Então, é possível interpretar o tensor de curvatura de Riemann como o modo de medir o quanto a variedade $�$ difere de um espaço euclidiano, ou de um espaço de Minkowski no contexto da relatividade. Logo, um espaço é dito plano quando o tensor de Riemann é zero.

Considerando um sistema de coordenadas $\{x^{i}\}$ , em que $X=\partial /\partial x^{i}$ e $Y=\partial /\partial x^{j}$ . Então, $[X,Y]=0$ e portanto a fórmula simplifica como

R(X,Y)Z=\nabla _{X}\nabla _{X}Z-\nabla _{Y}\nabla _{X}Z

ou seja, neste caso o tensor de curvatura mede a não-comutatividade da derivada covariante.^[2]

Expressão em coordenadas

Considerando a base coordenada $\{\mathbf {e} _{\mu }\}$ e sua correspondente dual $\{\mathrm {d} x^{\kappa }\}$ , o tensor de Riemann pode ser expresso como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{R^{\kappa }}_{\lambda \mu \nu }=\left\langle \mathrm {d} x^{\kappa },R\left(\mathbf {e} _{\mu },\mathbf {e} _{v}\right)\mathbf {e} _{\lambda }\right\rangle =\left\langle \mathrm {d} x^{\kappa },\nabla _{\mu }\nabla _{\nu }\mathbf {e} _{\lambda }-\nabla _{\nu }\nabla _{\mu }\mathbf {e} _{\lambda }\right\rangle

em que $\langle .,.\rangle$ representa o produto interno.

Deste modo, a expressão pode ser representada em termos de coordenadas usando os símbolos de Christoffel. Valendo-se da convenção do somatório de Einstein, pode-se representá-lo como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{R^{\kappa }}_{\lambda \mu \nu }={\partial _{\mu }{\Gamma ^{\kappa }}_{\nu \lambda }}-{\partial _{\nu }{\Gamma ^{\kappa }}_{\mu \lambda }}+{\Gamma ^{\eta }}_{\nu \lambda }{\Gamma ^{\kappa }}_{\mu \eta }-{\Gamma ^{\eta }}_{\mu \lambda }{\Gamma ^{\kappa }}_{\nu \eta }

sendo $\nabla _{v}\mathbf {e} _{\lambda }={\Gamma ^{\eta }}_{\nu \lambda }\mathbf {e} _{\eta }$ .^[3]

Comutadores e índices

Dado um quadrivetor genérico $�$ , o tensor de Riemann surge da comutação da derivada covariante segunda desse quadrivetor, ou seja,^[4]

[\nabla _{\mu },\nabla _{\nu }]A^{\rho }=\nabla _{\mu }\nabla _{\nu }A^{\rho }-\nabla _{\nu }\nabla _{\mu }A^{\rho }={R^{\rho }}_{\sigma \mu \nu }A^{\sigma }-{T^{\lambda }}_{\mu \nu }\nabla _{\lambda }A^{\rho }

no qual ${T^{\lambda }}_{\mu \nu }$ é o tensor de torção.

Considerando o caso em que não há torção, isto é,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[\nabla _{\mu },\nabla _{\nu }]A^{\rho }={R^{\rho }}_{\sigma \mu \nu }A^{\sigma }

o tensor de Riemann expressa a diferença medida da curvatura da variedade $�$ quando o vetor $�$ é transportado do ponto $�$ para um ponto $�$ , primeiramente ao longo de uma congruência, e depois seguindo outra congruência, ou vice-versa.^[5]

Versão covariante

O tensor métrico covariante $g_{\rho \zeta }$ pode se usado para abaixar um índice do tensor de Riemann, assim como o tensor contravariante $g^{\rho \zeta }$ pode levantar um índice. Assim, a versão completamente covariante do tensor de curvatura do tipo (0,4) é dada por

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

R_{\rho \sigma \mu \nu }=g_{\rho \zeta }{R^{\zeta }}_{\sigma \mu \nu }.

Propriedades

Simetrias algébricas

O tensor de Riemann é antissimétrico nos dois últimos índices, ou seja,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{R^{\rho }}_{\sigma \mu \nu }=-{R^{\rho }}_{\sigma \nu \mu }

R_{\rho \sigma \mu \nu }=-R_{\rho \sigma \nu \mu }

Na sua forma completamente covariante, o tensor de Riemann é antissimétrico em relação à troca dos dois primeiros índices, isto é,

R_{\rho \sigma \mu \nu }=-R_{\sigma \rho \mu \nu }

e é simétrico em relação à troca do primeiro par de índices com o segundo:

R_{\rho \sigma \mu \nu }=R_{\mu \nu \rho \sigma }

Primeira identidade de Bianchi

Na ausência de torção, temos:

R_{\rho \sigma \mu \nu }+R_{\rho \nu \sigma \mu }+R_{\rho \mu \nu \sigma }=0

Esta relação também pode ser escrita mais como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

R_{\rho [\sigma \mu \nu ]}=0

em que $[\sigma \mu \nu ]$ indica uma antissimetrização nos índices. Assim, deve-se efetuar uma soma sobre todas as permutações dos três últimos índices, com um sinal correspondente à paridade da permutação. Resultando em 6 termos, mas que podem ser acoplados em virtude das propriedades algébricas descritas acima.

Componentes independentes

Embora o tensor de Riemann tenha $n^{4}$ componentes, em que $�$ é a dimensão da variedade sobre qual o tensor é definido, as relações descritas anteriormente reduzem este número a ${\frac {1}{12}}n^{2}(n^{2}-1)$ componentes independentes. Para duas, três e quatro dimensões, o número de componentes independentes é respectivamente 1, 6 e 20.^[6]

Segunda identidade de Bianchi

A segunda identidade de Bianchi é parecida com a primeira, mas leva em consideração a derivada covariante do tensor de Riemann. Na ausência de torção, a identidade possui a seguinte forma:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\nabla _{\lambda }R_{\rho \sigma \mu \nu }+\nabla _{\rho }R_{\sigma \lambda \mu \nu }+\nabla _{\sigma }R_{\lambda \rho \mu \nu }=0

Essa igualdade pode ser escrita de forma mais concisa como^[4]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\nabla _{[\lambda }R_{\rho \sigma ]\mu \nu }=0

Tensor de curvatura de Ricci

O tensor de curvatura de Ricci é a contração do primeiro e terceiro índice do tensor de Riemann.

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\underbrace {\operatorname {R} _{ab}} _{\text{Ricci}}\equiv \underbrace {\operatorname {R} ^{c}{}_{acb}} _{\text{Riemann}}=g^{cd}\underbrace {\operatorname {R} _{cadb}} _{\text{Riemann}}

Pesquisar este blog

MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [742]

Escalares simples na relatividade especial

O comprimento de um vetor de posição

O comprimento de um vetor de velocidade

O produto interno da aceleração e da velocidade

Energia, massa em repouso, trimomento e trivelocidade a partir do quadrimomento

Medição da energia de uma partícula

Medição da massa de repouso da partícula

Medição do trimomento da partícula

Medição da trivelocidade da partícula

Escalares mais complicados

Relação com a ação Nambu-Goto

Definição

Folha de universo

Descrição

Definição geral

Expressão em coordenadas

Comutadores e índices

Versão covariante

Propriedades

Simetrias algébricas

Primeira identidade de Bianchi

Componentes independentes

Segunda identidade de Bianchi

Tensor de curvatura de Ricci

Comentários

Postar um comentário

Postagens mais visitadas deste blog